📢 공지합니다
이 게시글은 메인 페이지에 항상 고정되어 표시됩니다.
사이트
https://www.acmicpc.net/problem/9095
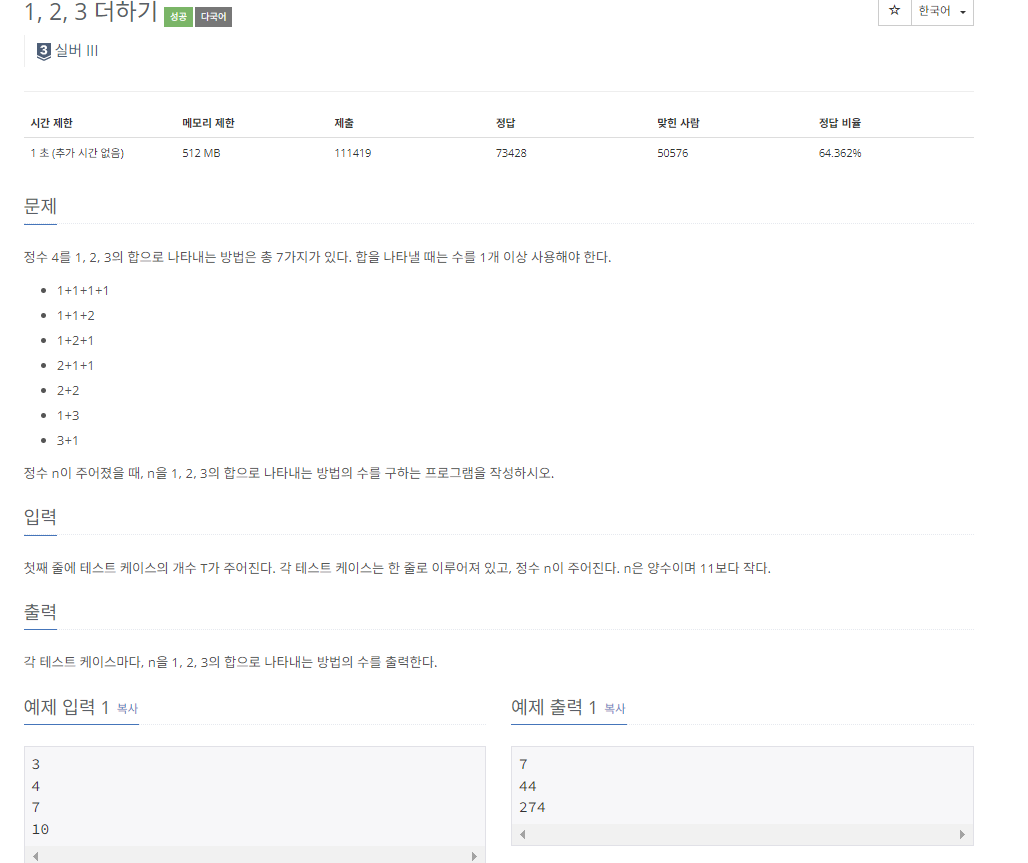
9095번: 1, 2, 3 더하기
각 테스트 케이스마다, n을 1, 2, 3의 합으로 나타내는 방법의 수를 출력한다.
www.acmicpc.net
문제
분석
문제를 처음에 잘못 읽어서 재귀함수로 계속 구현하다가 결국 도움을 받았다... 반성하자.
일단 DP는 필자가 굉장히 어려워하는 알고리즘이다. DP는 먼저 점화식을 세우는게 우선이다.
1,2,3만 더해서 만들 수 있는 경우의 수를 구하는 것이다.
1=(1)
2=(1+1, 2)
3=(1+1+1, 1+2, 2+1, 3)
4=(1+1+1+1, 1+2+1, 2+1+1, 1+1+2, 2+2, 3+1, 1+3) 쭉 이렇게 간다. 여기서 자세히 보면 규칙이 나온다.
4는 1,2,3의 경우의 수가 다 더해져서 나온것이다.
즉 규칙을 잘보면 4= 3+1, 2+2, 1+3 로 해석이 될 수 있다.
5= 4+1, 3+2, 2+3
6= 5+1, 4+2, 3+3
7= 6+1, 5+2, 4+3
8= 7+1, 6+2, 5+3 -> 이때 여기서 4는 왜 뺏냐는 의문이 많을 것이다. 이유는 당연히 1,2,3으로 만 더해야 되므로 뺀것이다.
애초에 5가 4를 포함해서 나온것이기 때문이다.
규칙이 많이 헷갈릴텐데 이해하면 쉬운 문제였다.
public class DP9095 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int t;
t = Integer.parseInt(br.readLine());
int dp[]=new int[11];
for (int i = 0; i < t; i++) {
int n=Integer.parseInt(br.readLine());
dp[0]=0;
dp[1]=1;
dp[2]=2;
dp[3]=4;
for(int j=4; j<n+1; j++){
dp[j]=dp[j-1]+dp[j-2]+dp[j-3];
}
System.out.println(dp[n]);
}
}
}
- n은 10이하이므로 dp배열을 11로 설정해 놓는다.
- dp 배열 1,2,3을 경우의 수로 배정해 놓는다.
- 그 후 j=4부터 해서 점화식을 이용해 n에 따라 배열에 값을 넣으면 된다.
- 저게 끝 전체 코드이다.
결과

느낀점
본격적인 DP입문시작! 그래프가 너무 쉬었다. 진짜..... 재귀함수가 너무 어렵다. 점화식도 어렵고... 열심히 해보자
그래프도 처음에 어려웠으니깐
| [백준] 10819번 (0) | 2024.02.01 |
|---|---|
| [백준] 1049번 (1) | 2024.01.22 |
| [백준] 14502번 (0) | 2023.11.13 |
| [백준] 7576번 (0) | 2023.11.10 |
| [백준] 1213번 (0) | 2023.10.31 |